The Sixth DIMACS Implementation Challenge:
Near Neighbor Searches

General Information

August 19, 1998 (revised timeline)

1 Introduction

In conjunction with its Special Year on Massive Data Sets, the Center for Discrete Mathematics and Theoretical Computer Science (DIMACS) invites participation in an Implementation Challenge focusing on Near Neighbor Searches. The Implementation Challenge will take place between January 1998 and January 1999. Participants are invited to carry out research projects related to the problem area and to present research papers at a DIMACS workshop to be held on January 15-16, 1999 in Baltimore, Maryland (in conjunction with ALENEX'99). A refereed workshop proceedings of the DIMACS Challenge workshop will be published as part of the AMS-DIMACS book series.

Finding near neighbors according to various distance measures arises in many application areas, including but not limited to finding similar web documents, images, DNA sequences, lines of text, or audio and video clips, and more generally in areas of statistics, data mining, information retrieval, pattern recognition and data compression. The goal of the Implementation Challenge is to determine how algorithms depend on the structure of the underlying data sets, as well as to determine realistic algorithm performance where worst case analysis is overly pessimistic and probabilistic models are too unrealistic. We invite research projects in the following two directions, discussed in greater detail in Section 2.

Providing Interesting Data Sets and Distance Measures. We invite researchers from various application areas to provide interesting data sets for near neighbor problems. Contributions could consist either of sample data sets from a true application or of realistic instance generators resembling practical data sets. Our goal is to construct a library of test problems that will be available for study both during and after the Challenge.

Developing Near Neighbor Algorithms. Neighbor algorithms may be developed either for specific application domains or for more general spaces. Algorithms may aim to find the nearest neighbor, several nearest neighbors, or approximate neighbors. Projects may involve either public domain or proprietary codes.

2 Research Problems

The emphasis of the Challenge is to consider various neighbor problems in the following static, online setting. An algorithm is first given access to a fixed data set, comprised of points from some underlying domain. After preprocessing the data set and generating any associated data structures, an algorithm will be given a sequence of new query points, and for each one, will be asked to find the neighbor(s) to the query in the original input space.

In some settings, very efficient data structures have been designed for these problems. For instance, for a metric space defined by the Euclidean distance between a set of points in the plane, structures such as the Voronoi diagram or quadtrees can be built, using linear storage and logarithmic query time. The focus of the Challenge is to better understand the realistic performance of algorithms as the data sets undergo a dramatic increase in size, and also as the underlying space increases in dimensionality or becomes non-Euclidean.

Through the rest of this section, we discuss possible variants for near neighbor problems. These variants suggest many possible research projects for the Implementation Challenge, however participation is not necessarily limited to these directions.

2.1 General Spaces vs. Application-specific Domains

Near neighbor problems arise in a variety of applications, based on data sets from very different domains (see Section 2.7 for a list of possible domains). A first question is whether it is possible to design very general algorithms and data structures which can be used across many applications, with data and distance functions that seemingly have nothing in common. A general algorithm for these problems may rely only on a black-box oracle for the similarity of two points. For example, previous researchers have consider such general algorithms which require only that a distance function satisfies the triangle inequality and thus forms a metric space [Bri95,Cla97,FS82,Uhl91,Yia93].

However, when examining a data set from a very specific application, much stronger results may be possible. One possibility is that the additional problem structure can be used to improve the performance for one of the general algorithms above. Alternatively, algorithms which have more knowledge of the underlying domain may be able to use the raw data to provide better solutions. For example, an important special case is when the data set consists of d-dimensional points in Euclidean space. Researchers have considered near neighbor queries for Euclidean spaces in both low and high dimensions [AM92,Ben75,Cla88,DL76,IMRV97,Kle97,Mat91,Mei93,Mul91,YY85].

2.2 Possible Queries and Responses

Given a query point q, the most traditional goal may be to return a point of the original data set which is closest to q. However there are many other related queries which could be asked. The following list contains many such questions, noting when possible previous research related to the particular query type. We welcome other suggestions for useful queries.

We define our queries based on the following subsets of the original data set, relative to q. For a given set, we can form a query which asks an algorithm to return a single member of the set, or a query which asks an algorithm to return the entire set.

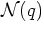${\cal N}(q)$ - The point which is the nearest to q (if not unique, the set of all points which are closest) [Cla88,Cla97,DL76,Mei93].
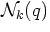${\cal N}_k(q)$ - The nearest k points to q (if not unique, the set of all points for which there are at most k-1 points nearer to q).
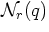${\cal N}_r(q)$ - All points within distance r or less from q [Bri95].
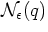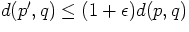${\cal N}_\epsilon(q)$ - If the true nearest point p has distance d(p,q), this set consists of all points p' for which $d(p',q) \leq (1+\epsilon)d(p,q)$ [AMN+94,Cla94,Cla97,Kle97].
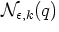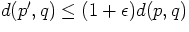${\cal N}_{\epsilon,k}(q)$ - If the kth nearest point p has distance d(p,q), this set consists of all points p' for which $d(p',q) \leq (1+\epsilon)d(p,q)$ .

We can consider combining the above sets, for instance asking an algorithm to return the entire set 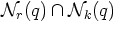${\cal N}_r(q) \cap {\cal N}_k(q)$ ,is equivalent to asking for the k nearest neighbor to q, except throwing out any of those which are at distance greater than r [IMRV97].

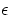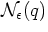Furthermore, we can consider approximate versions of the problems, for instance having an algorithm minimizing the value of $\epsilon$ , while being able to return a member of ${\cal N}_\epsilon(q)$ .

Finally, we can also consider Monte Carlo, randomized algorithms for all of these queries, attempting to maximize the probability that the response to a query is legitimate.

2.3 Source of Query Points

Algorithms may consider query points which are supplied in one of several ways. They may be chosen arbitrarily by a user. They may be chosen by the same random distribution which supplied the original data set. Or they may be chosen by a separate random distribution, however an algorithm may be supplied with a small sample of these queries during the preprocessing step.

2.4 Classification Systems

In a classification system, we assume that all of the original data points are colored, and rather than asking about the exact input point which is closest to some query q, we can instead ask what color is the point nearest to q. In fact, for all of our query sets defined in Section 2.2, we can ask corresponding classification queries, asking either for the majority color within a set or for the exact color distribution within a set.

2.5 Using Approximate Distance Functions

In applications where computing the true distance function is quite expensive, we could consider the use of algorithms which try to make use of inaccurate distance functions which may be computed more efficiently. For instance, one could consider a secondary function which returns the distance as long as it is less than some threshold T, but returns infinity otherwise, or a secondary function which is monotone in the true distance function. Alternatively, it may be that distance values are cached, and so a secondary function may be able to return the exact distance quickly, so long as that distance is in the cache.

2.6 Use of Near Neighbor Algorithms in Other Applications

Another direction for research is to look at applications in which a nearest neighbor algorithm is used as a black box procedure for a larger algorithm. For example, many clustering algorithms build their clusters using nearest neighbor queries, for instance adding points to the clusters based on their distance to the clusters, or merging together clusters based on the distance between their centers. Similarly, nearest neighbor queries are used by a common heuristic for building traveling salesmen tours. Experimentation could be done to understand how different nearest neighbor algorithms effect the performance of the larger program.

2.7 Problem Domains

Text Strings -- We could search a fixed dictionary to find nearby words for a mis-spelled word. Or we could search an essay for lines which are nearly plagiarized from some other source. The distance functions on words or lines could be based on Hamming distance or on a variety of edit distances.
Documents -- We could search a collection of documents for ones which are closely related to a given query document. For instance, we may ask to find similar web pages, or relevant news articles. Distance functions could be based on a vector of word frequency counts, or in the case of web pages on the incoming or outgoing links. A useful classification system may have a large training set of both spam and non-spam email messages, and then given a new message, it could predict whether the nearby messages are labeled as spam or non-spam.
DNA Sequences -- Given a large collection of DNA sequences, for example an evolutionary tree, we may wish to find neighbors of a new sample, or to classify a new sample based on the collection.
Images -- A library of images can be searched, where similarity is based on some combination of properties such as colors, features, embedded text, and so on.
Audio streams -- Can we identify a speaker by comparing a sample to a database of speakers.
Video streams -- Can we find similarity between different video clips, or between frames of the same clip?
Bibliographies -- Can we find articles related to a query, based on a combination of authors, titles, abstracts, etc.?

2.8 Evaluating Algorithm Performance

One of the main issues in the DIMACS Implementation Challenges is in using experimentation alongside theoretic analysis in determining realistic algorithm performance. Using various data sets provided by participants, we will later list a set of benchmarks which other participants may use to evaluate various search algorithms.

There are four main axes for evaluating the performance of an algorithm, namely the preprocessing time, the preprocessing space, the query time, and in the case of approximate searches, the quality of the solution. Of course along each axis, there are many possible ways to evaluating the performance. For algorithms acting on general spaces, the number of calls to the distance oracle is one very natural atomic operation for measuring the preprocessing and query running times. For algorithms specialized to a domain, other atomic operations may provide natural measures of performance.

Furthermore, participants may wish to compare overall running times for algorithms under similar conditions. Besides testing an algorithm on the given queries, participants may want to run additional experiments by finding all nearest neighbors within the original data set, finding the closest pair of points in the original data, or finding the site which is most isolated from all others.

3 How to Participate

The Challenge began in January 1998 and will conclude with a Workshop in January of 1999. The only firm deadline in the Challenge will be for the submission of extended abstracts for the Workshop on or before September 11, 1998. Later deadlines will be set for submission of the full paper for the refereed proceedings.

However, the goal of this Challenge is to use the period between January 1998 and January 1999 to provide feedback and interaction for ongoing research. It is during this period that the Steering Committee will be reviewing short abstracts and suggesting alternative approaches. It is also during this period that researchers will be able to coordinate and interact with others doing similar work.

As of August 1998, the remainder of the Challenge schedule is as follows:

September 11, 1998:
Deadline for submitting an extended abstract (up to ten pages), from which the Implementation Challenge Workshop presenters will be chosen by the Challenge Steering Committee. Extended abstracts should be submitted by either one of the two following methods:

1.
Six hard copies of the abstract can be sent to,
Michael Goldwasser
Dept. of Computer Science
35 Olden Street
Princeton, NJ 08544
2.
Alternatively, postscript versions of the abstract can be submitted electronically to challenge6@dimacs.rutgers.edu.
October 1998:
Steering Committee will announce the list of those abstracts which were accepted for presentation in the Implementation Challenge Workshop. Soon after this, the set of accepted extended abstracts for the Implementation Challenge will be circulated to those with accepted presentations. This will allow participants to prepare their workshop presentation with the related papers already in mind and it will encourage further communication between participants.
October 1998 - January 1999:
Those accepted as presentors at the Challenge Workshop are free to continue experiments in preparation for their presentations. Throughout this period, we will continue to gather contributed data sets and algorithms at the Challenge web page. Additionally we welcome further communication between participants during this time.
January 15-16, 1999:
The DIMACS Implementation Challenge Workshop will be held in coordinate with ALENEX'99 in Baltimore, Maryland at the Baltimore Omni Inner Harbor Hotel (For more details on the rest of ALENEX'99, please see their web page at http://www.cs.jhu.edu/Conferences/ALENEX99/).
March 1999 (tentative):
Full papers will be due for consideration in the refereed Implementation Challenge proceedings in the AMS-DIMACS book series. Please note, only those papers which were presented at the Workshop will be eligible for publication in the proceedings.

Support code, program development and testing tools, and data sets may be submitted and are welcome at any time. Throughout the challenge, submitted algorithms and data sets will be made available on the Challenge web page, with the contributor's permission.

3.1 Online Information

All information for the Challenge will be available online, through the Sixth Implementation Challenge Web page
(http://www.dimacs.rutgers.edu/Challenges/Sixth/). Additionally, most information will be available through ftp (dimacs.rutgers.edu:/pub/challenge6/). Any additional questions can be sent to the organizers at (challenge6@dimacs.rutgers.edu).

3.2 DIMACS Support

DIMACS facilities will provide a clearing-house for exchange of programs and data and for communication among researchers, including a collection of benchmark instances and evaluation criteria for algorithms. A steering committee offers the participants advice and support in their projects throughout the duration of the implementation challenge. DIMACS can provide neither financial support for research projects nor machine cycles for the experiments. Full or partial support for travel and expenses may be available for those presenting at the Workshop.

3.3 Steering Committee

The following people are serving on the Steering Committee for the Sixth Challenge, helping to set the guidelines for participation:

Jon Bentley, Bell Labs (jlb@research.bell-labs.com),
Ken Clarkson, Bell Labs (clarkson@research.bell-labs.com),
Michael Goldwasser (coordinator), Princeton University (wass@cs.princeton.edu),
David Johnson, AT&T Labs (dsj@research.att.com),
Cathy McGeoch, Amherst College (ccm@cs.amherst.edu),
Robert Sedgewick, Princeton University (rs@cs.princeton.edu).

References

AM92

Pankaj Agarwal and Jirí Matousek.
Ray shooting and parametric search.
In Proc. 24th ACM Symp. Theory Comp., pages 517-526, 1992.

AMN+94

Sunil Arya, David Mount, Nathan Netanyahu, Ruth Silverman, and Angela Wu.
An optimal algorithm for approximate nearest neighbor searching.
In Proc. 5th ACM Symp. on Discrete Algorithms, pages 573-583, 1994.

Ben75

Jon L. Bentley.
Multidimensional binary search trees used for associative searching.
Communication of the ACM, 18(9):509-517, 1975.

Ben80

J. L. Bentley.
Multidimensional divide-and-conquer.
Commun. ACM, 23(4):214-229, 1980.

Bri95

Sergey Brin.
Near neighbor search in large metric spaces.
In Proc. 21st Inter. Conf. on Very Large Data Bases, pages 574-584, 1995.

BS76

J. L. Bentley and M. I. Shamos.
Divide-and-conquer in multidimensional space.
In Proc. 8th Annu. ACM Sympos. Theory Comput., pages 220-230, 1976.

BWY80

J. L. Bentley, B. W. Weide, and A. C. Yao.
Optimal expected-time algorithms for closest-point problems.
ACM Trans. Math. Softw., 6:563-580, 1980.

Cla88

Kenneth Clarkson.
A randomized algorithm for closest-point queries.
SIAM J. Comput., 17(4):830-847, 1988.

Cla94

Kenneth Clarkson.
An algorithm for approximate closest-point queries.
In Proc. 10th ACM Symp. on Computational Geometry, pages 160-164, 1994.

Cla97

Kenneth Clarkson.
Nearest neighbor queries in metric spaces.
In Proc. 39th ACM Symp. Theory Comp., pages 609-617, 1997.

DDS92

M. T. Dickerson, R. L. Drysdale, and J. R. Sack.
Simple algorithms for enumerating interpoint distances and finding k nearest neighbors.
Internat. J. Comput. Geom. Appl., 2(3):221-239, 1992.

DL76

David Dobkin and Richard Lipton.
Multidimensional searching problems.
SIAM J. Comput., 5(2):181-186, 1976.

FS82

C. Feustel and L. Shapiro.
The nearest neighbor problem in an abstract metric space.
Pattern Recognition Letters, 1:125-128, 1982.

IMRV97

Piotr Indyk, Rajeev Motwani, Prabhakar Raghavan, and Santosh Vempala.
Locality-preserving hashing in multidimensional spaces.
In Proc. 39th ACM Symp. Theory Comp., pages 618-625, 1997.

Kle97

Jon Kleinberg.
Two algorithms for nearest-neighbor search in high dimensions.
In Proc. 39th ACM Symp. Theory Comp., pages 599-608, 1997.

Mat91

Jirí Matousek.
Reporting points in halfspaces.
In Proc. 32nd Symp. on Found. Comput. Sci., pages 207-215, 1991.

Mei93

Stefan Meiser.
Point location in arrangements of hyperplanes.
Information and Computation, 106(2):286-303, 1993.

MS97

Nimrod Megiddo and Uri Shaft.
Efficient nearest neighbor indexing based on a collection of space filling curves.
Technical Report IBM Research Report RJ 10093 (91909), IBM Almaden Research Center, San Jose California, 1997.

Mul91

Ketan Mulmuley.
Randomized multidimensional search trees: Further results in dynamic sampling (extended abstract).
In Proc. 32nd Symp. on Found. Comput. Sci., pages 216-227, 1991.

Sam89

Hanan Samet.
The Design and Analysis of Spatial Data Structures.
Addison-Wesley, Reading, Ma, 1989.

Uhl91

Jeffrey K. Uhlmann.
Satisfying general proximity/similarity queries with metric trees.
Information Processing Letters, 40(4):175-179, 1991.

Vai89

P. M. Vaidya.
An algorithm for the all-nearest-neighbors problem.
Discrete and Computational Geometry, 4:101-115, 1989.

Yia93

Peter Yianilos.
Data structures and algorithms for nearest neighbor search in general metric spaces.
In Proc. 4th ACM Symp. on Discrete Algorithms, pages 311-321, 1993.

YY85

Andrew Yao and Frances Yao.
A general approach to d-dimensional geometric queries.
In Proc. 17th ACM Symp. Theory Comput., pages 163-168, 1985.

Sixth DIMACS Implementation Challenge.

Previous DIMACS Implementation Challenges.

DIMACS Home Page.

Maintained by Michael Goldwasser
challenge6@dimacs.rutgers.edu
Document last modified on August 19, 1998.

The Sixth DIMACS Implementation Challenge: Near Neighbor Searches

General Information

August 19, 1998 (revised timeline)

The Sixth DIMACS Implementation Challenge:
Near Neighbor Searches